神经网络笔记1

对比线性代数算法

基础的线性代数算法 s = Wx, x 是一个输入矩阵 [n 1], W 是一个权重矩阵 [种类 n]，s 为一个评分矩阵。

神经网络算法简介

神经网络算法是 s = W_2 max(0, W_1x). 在这种情况下 W_1 广度增加，比如可能为 [100 * n], max 是通过设置熵值来过滤掉所有的小于0的score。其实有其他方法来过滤。

W_2 是一个[种类 * 100] 的矩阵，权重W 通过梯度下降来学习。

单个神经元建模

神经网络是从生物上得到的启发。

生物动机与连接

!()[https://pic4.zhimg.com/80/d0cbce2f2654b8e70fe201fec2982c7d_hd.jpg]

当多个信号传进神经元，与神经元内权重相乘并且相加，如果超过某一个阈值，那么激活神经元。激活函数最早接触的sigmoid，最大优势是将数据控制在【0，1】之间。

一个神经元前向传播的代码是：

class Neuron(object):
	# ... 
	def forward(inputs):
	  """ 假设输入和权重是1-D的numpy数组，偏差是一个数字 """
	  cell_body_sum = np.sum(inputs * self.weights) + self.bias
	  firing_rate = 1.0 / (1.0 + math.exp(-cell_body_sum)) # sigmoid激活函数
	  return firing_rate

—- Todo —–

作为线性分类器的单个神经元

分类器我的理解还是吧score 转化为正确概率。然后进行一个loss 的计算, 前面有公式

二分类Softmax分类器

二分类SVM分类器

分类器	公式	优点	缺点
Softmax分类器	softmax函数	和为1	较慢的学习曲线，所有的结果都有loss
SVM分类器	在0和得分差中选最大值	更快的去除一些失误值	有时候学习会卡住

常用激活函数

我的理解，激活函数就是通过score 得到概率。

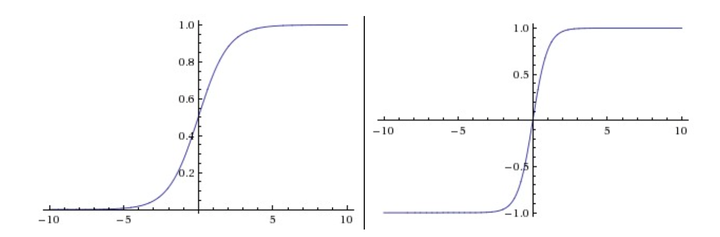
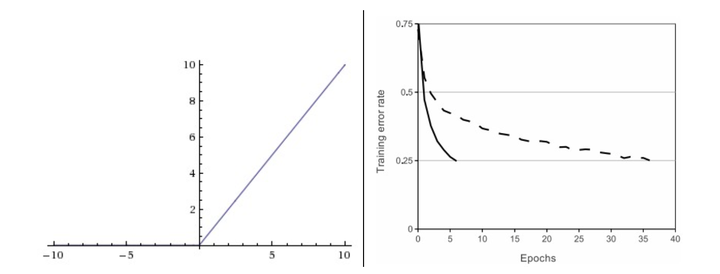
激活函数	优点	缺点
Sigmoid	简单，易理解	Sigmoid函数饱和使梯度消失，输出不是零中心的
Tanh	输出不是零中心的，易理解	有时候会
ReLU	1. 线性，非饱和的公式，随机梯度下降的收敛有巨大的加速 2，耗费较少计算资源的操作	学习率太高的时候，这个ReLU单元在训练中将不可逆转的死亡
Leaky ReLU	同上，并且解决了ReLu单元死亡的问题	然而该激活函数在在不同任务中均有益处的一致性并没有特别清晰（不太懂）
Maxout	有以上所有的优点	参数过多

神经网络结构

最普通的层的类型是全连接层（fully-connected layer）

命名规则 N层神经网络 = hidden layer + output layer
输出层大多用于表示分类评分值
网络尺寸标准主要有两个：一个是神经元的个数，另一个是参数的个数

前向传播

# 一个3层神经网络的前向传播:
f = lambda x: 1.0/(1.0 + np.exp(-x)) # 激活函数(用的sigmoid)
x = np.random.randn(3, 1) # 含3个数字的随机输入向量(3x1)
h1 = f(np.dot(W1, x) + b1) # 计算第一个隐层的激活数据(4x1)
h2 = f(np.dot(W2, h1) + b2) # 计算第二个隐层的激活数据(4x1)
out = np.dot(W3, h2) + b3 # 神经元输出(1x1)

神经网络最后一层通常是没有激活函数的, 得出一个实数值的评分

表达能力

至少拥有一个隐层(hidden)的神经网络是一个通用的近似器，神经网络可以近似任何连续函数。

实践而言，构建更多层的神经网络所表达出来的函数不仅平滑，而且更容易学习（利用最优化）

设置层的数量和尺寸

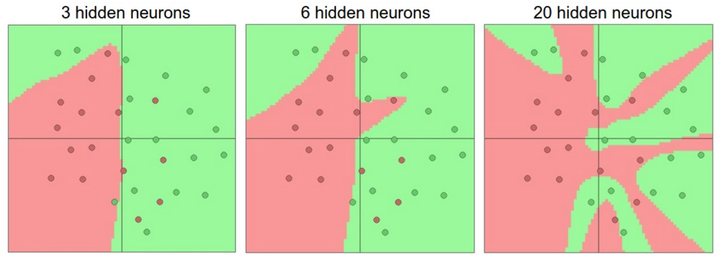
更大的神经网络可以表达出更复杂的函数,但是缺点是过拟合(overfitting),只是重视数据在复杂情况中的分类，而忽略了潜在关系。

这时候合适的layer可以在测试数据里获得更好的泛化(generalization)能力

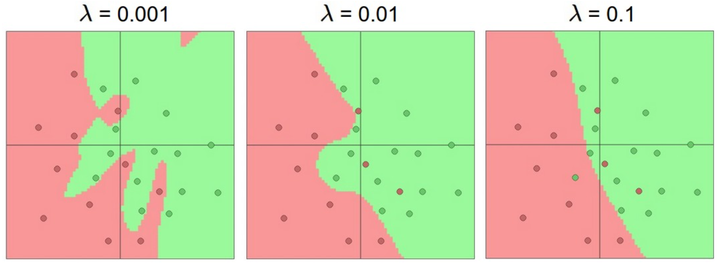
然而, 防止神经网络过拟合的方法有很多(To learn), 选择其他过拟合的解决方法，而不应该去选择小的神经网络。

这个是提供的测试的链接convnetjs DEMO

Reference

convnetjs DEMO

神经网络笔记1（上）

神经网络笔记1（下）

Weijie Sun Blog

cs231n-note-5

神经网络笔记1

对比线性代数算法

神经网络算法简介