PCA的数学原理
PCA(Principal Component Analysis)是一种常用的数据分析方法(降维)
1. 数据的向量表示及降维问题
我们要在降维的同时让数据信息资源的损失尽可能降低.
朴素降维思考,比如男女column, M F,可以去掉一列,因为非黑即白。
eg: 数据记录为
(日期, 浏览量, 访客数, 下单数, 成交数, 成交金额) => (500,240,25,13,2312.15)T
比如浏览量和访客数是有关联的,可以简单降维
2. 向量的表示及基变换
3. 内积与投影
内积, 高中学的叫点乘,或者还看见有人叫点积(Dot Product)
$ \vec A \vec B = a_1 x b_1 + … + a_n x b_n $
在几何定义为向量A 和 向量B的长度 乘以 cos(夹角)如果B的模长度为1,那么AB 的点乘就是A 投影在B上的长度
$ \vec A \vec B = \left\lvert \vec A \vec B \right\rvert x cos(\theta) $
4. 基 basis)
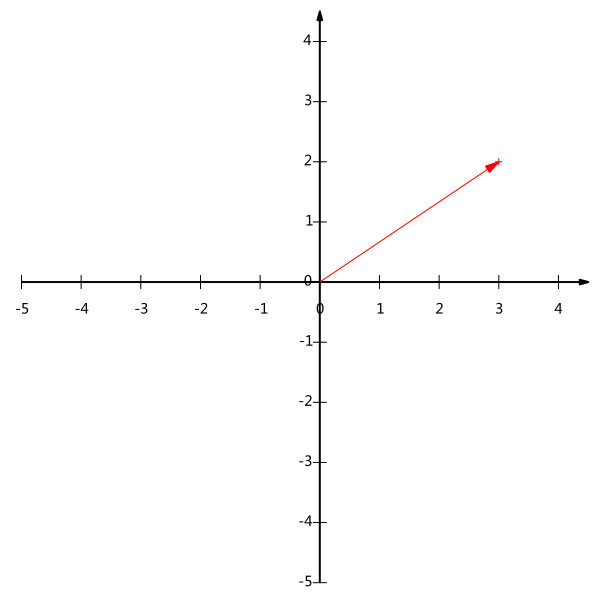
原理上是在x轴上的投影为3,在y轴上的投影为2。 从代数原理上,(3,2) = 3x(1,0)+2x(0,1)
(1,0) 和 (0,1) 就是二维空间中的一组基,基的模长度往往为1
我们可以变换这组基的方向,比如(1,1), (-1,1),然后把他转化为基,即为 (\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})和(-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}})。
基变换 (二维)
顺时针 theta 角度
cos(theta) -sin(theta)
sin(theta) cos(theta)
5. 基变换的矩阵表示
原坐标 [1 0], [0 1]
[1 0] [3] => [3]
[0 1] [2] [2]
新坐标
$$ (\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}) $$
$$ (-\frac{1}{\sqrt{2}},\frac{1}{\sqrt{2}}) $$
当把M个N维向量变换到R个N维向量表示的新空间中去,数学表达式为
R是可以小于N的,R是基的数量,可以讲N维数据变换到更低的维度中去。这种矩阵相乘表示为降维变换。
6. 协方差矩阵及优化目标
关于如何选择最优的基,比如从N维向量降维到K。
例子 把五条2维向量 降维到 1维空间
(1,1) (1,3) (2,3) (4,4) (2,4)
先减去均值
(-1,-2) (-1,0) (0,0) (2,1) (0,1)
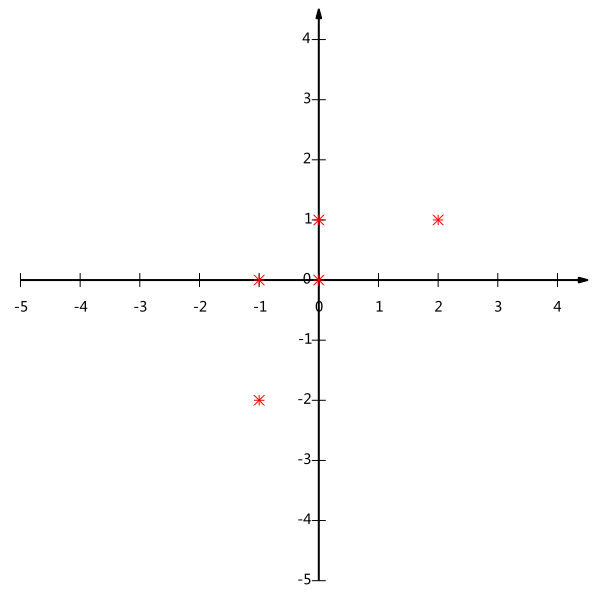
如果选一条线当一维坐标,如果选X轴(0,1) (0,0) 重叠, 如果选y轴(-1,0), (0,0) 重叠
我的理解是应该选一种空间 让每个投影都尽量分散
7. 方差
$$ Var(a)=\frac{1}{m}\sum_{i=1}^m{(a_i-\mu)^2} $$
上面提到的问题变成寻找一个一维基上投影的点方差最大
8. 协方差
如果降到二维,还是坚持最大方差的话那么第二条线会与第一条线重合,但是最理想情况是第二条线和第一条线独立。
协方差
$$ Cov(a,b)=\frac{1}{m}\sum_{i=1}^m{a_ib_i} $$ 当协方差为0的时候两个向量完全独立,也就是正交(是垂直吗?)
至此,我们得到了降维问题的优化目标:将一组N维向量降为K维(K大于0,小于N),其目标是选择K个单位(模为1)正交基,使得原始数据变换到这组基上后,各字段两两间协方差为0,而字段的方差则尽可能大(在正交的约束下,取最大的K个方差)。
9. 协方差矩阵
(数学真是太有意思了)
假设我们有两个字段a,b, 我们把它们按行组成矩阵 X
$$ X=\begin{pmatrix} a_1 & a_2 & \cdots & a_m \ b_1 & b_2 & \cdots & b_m \end{pmatrix} $$
然后自己相乘并乘上系数
$$ \frac{1}{m}XX^\mathsf{T}=\begin{pmatrix} \frac{1}{m}\sum_{i=1}^m{a_i^2} & \frac{1}{m}\sum_{i=1}^m{a_ib_i} \ \frac{1}{m}\sum_{i=1}^m{a_ib_i} & \frac{1}{m}\sum_{i=1}^m{b_i^2} \end{pmatrix} $$
结果大概是
[a方差, 协方差]
[协方差, b方差]
10. 协方差矩阵对角化
于是根据上面的推导,我们要让对角线上的数据尽可能的高,因为方差变大,然后非对角线的协方差尽可能的小,因为每个基要独立。这样就达成了优化的条件。
接下来有点难懂:我先把每个数据都列下来
m为字段数(我的理解是需要投影的点)
n为基的维度 (我的理解是原数据的维度:可能错)
X 为基组成的矩阵 m x n
C 为一个对称矩阵
P 为行向量基组成的矩阵 r x m (r是什么:r可能是下降后的基的数目)
Y = PX Y是P投影在空间X上,X对P做的基变换
$$ \begin{array}{l l l} D & = & \frac{1}{m}YY^\mathsf{T} \ & = & \frac{1}{m}(PX)(PX)^\mathsf{T} \ & = & \frac{1}{m}PXX^\mathsf{T}P^\mathsf{T} \ & = & P(\frac{1}{m}XX^\mathsf{T})P^\mathsf{T} \ & = & PCP^\mathsf{T} \end{array} $$
要找到P,满足 $$ PCP^\mathsf{T} $$ 是一个对角矩阵
$$ PCP^\mathsf{T} $$ 对角元素从大到小排列,降到K维就取K行
实对称矩阵
协方差矩阵 C 是一个实对成矩阵(还未消化)
1 - 实对称矩阵不同特征值对应的特征向量必然正交。
2 - 设特征向量lambda重数为r,则必然存在r个线性无关的特征向量对应于lambda,因此可以将这r个特征向量单位正交化。
P是协方差矩阵的特征向量单位化后按行排列出的矩阵,其中每一行都是C的一个特征向量,
P按照D中特征值的从大到小排列,P的前K行组成的矩阵乘以原始数据矩阵X,就得到了我们需要降维后的矩阵Y
11. 算法及实例
总结一下PCA的算法步骤:
设有m条n维数据。
1)将原始数据按列组成n行m列矩阵X
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)$$ 求出协方差矩阵C=\frac{1}{m}XX^\mathsf{T} $$
4)求出协方差矩阵的特征值及对应的特征向量 特征值向量求法
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6)Y=PX即为降维到k维后的数据
举例那个去reference里面看更清楚,准备翻译成 IPython 更清晰解释PCA 降维
